Mkdir700's Note

Mkdir700's Note

小试牛刀-利用AST平坦化一段瑞数代码

爬虫
1809
2021-06-16

前言

最近一直在学习AST相关的知识，本篇文章就来小小的尝试下，利用AST平坦化控制流。

正常的执行逻辑： a -> b -> c

混淆后的执行逻辑则可能是这样：a -> d -> b -> d -> c -> d

正常流程

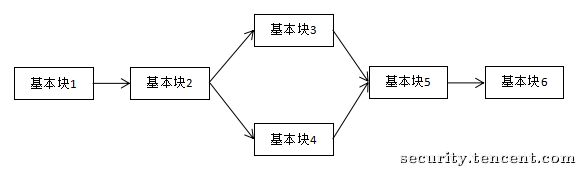
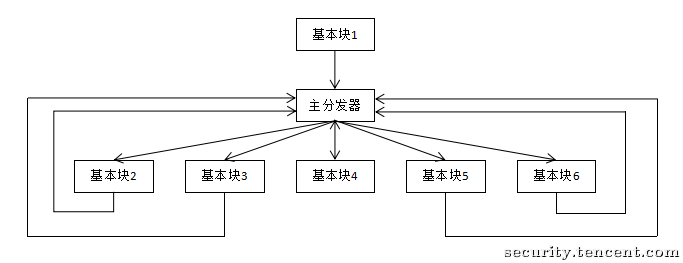
混淆后的流程

下方是从瑞数中提出的一段代码。

源代码

function func (_$eE) {
  var _$0n, _$2L, _$sC, _$o9, _$NU, _$qo, _$hK;
  var _$tg, _$DM, _$ZZ = 0, _$Ce = [7, 3, 4, 0, 9, 2, 8, 6, 1, 5];
  while (1) {
    _$DM = _$Ce[_$ZZ++];
    if (_$DM < 4) {
      if (_$DM < 1) {
        _$tg = !_$NU;
      } else if (_$DM < 2) {
        _$Uy(0);
      } else if (_$DM < 3) {
        _$NU = _$sC['$_ts'] = {};
      } else {
        _$sC = window, _$hK = String, _$o9 = Array;
      }
    } else if (_$DM < 8) {
      if (_$DM < 5) {
        _$NU = _$sC['$_ts'];
      } else if (_$DM < 6) {
        _$ZZ += -3;
      } else if (_$DM < 7) {
        return;
      } else {
        _$0n = [4, 16, 64, 256, 1024, 4096, 16384, 65536];
      }
    } else {
      if (_$DM < 9) {
        _$ZZ += 1;
      } else {
        if (!_$tg) _$ZZ += 1;
      }
    }
  }
}

先简单介绍上方代码的怎么执行的。

  1. 有一个整数数组和下标起始值（在本例中，起始值是_$ZZ=0）

  2. 进入while循环后，通过下标值去数组中取出一个整数，这个整数将经历多次判断，最终执行一条语句。

第一式：鬼影迷踪

纵使直接在while循环中调试比较复杂，但是执行过的语句总是会留下痕迹。

不知道小伙伴是否看过《三体》，其中的曲率引擎飞船达到光速后会在身后留下“死线”，这条“死线”也就是飞船的航行轨迹。

我们可以在while循环中，加入一些语句，记录下它的执行轨迹。

  var _$tg, _$DM, _$ZZ = _$eE, _$Ce = _$2z[0];
  window.trace = [];
  while (1) {
    _$DM = _$Ce[_$ZZ++];
    window.trace.push(_$DM)

当执行完毕之后，查看window.trace就可以看到它的执行轨迹了。

最终通过执行轨迹就可以知道它具体执行了哪些语句。

Tips：
如果函数存在递归，直接加入window.trace就不可行了，此时需要加入判定条件，比如判断递归的层数。

这个方法是我自己的胡乱瞎搞的，只是针对非常简单的情况，所以这里就不写详细的过程了。其实，我也更推荐第二种方法，第二种方法是我看**@Nanda** 文章总结出来的，也可以关注下这位大佬的公众号《爬虫术与道 》

第二式：森罗万象

相比“鬼影迷踪”，我更推荐“森罗万象”。这将包含所有情况，并且一旦完成可以说是一劳永逸。

因为_$DM的值决定了执行流程，所以我们可以动态维护_$DM，将整个流程走完就可以拿到所有执行的语句。

需要使用到以下模块：

const parser = require("@babel/parser");
const traverse = require("@babel/traverse").default;
const t = require("@babel/types")
const generator = require("@babel/generator").default;
const path = require("path");
const fs = require("fs");
let os = require("os");

处理逻辑

先把大致逻辑写出来：

  1. 将if...else if...else 转为if...else语句；

  2. 补全if...else...的大括号；

  3. 平坦化；

fs.readFile(path.resolve(__dirname, './source.js'), {'encoding': 'utf-8'}, function (err, data) {
  const ast = parser.parse(data);

  // 将if...else if...else语句转为if...else语句
  step1(ast);

  // 给没有括号的if...else语句加上括号
  step2(ast);
  
  // 平坦化
  step3(ast);

  let code = generator(ast).code;
  fs.writeFile('./result.js', code, {'encoding': 'utf-8'}, (err) => {
    console.log(err);
  })
})

Step1-处理if...else if...

先来看一下需要实现什么效果。

if (1) {
  console.log(1);
} else if (2) {
  console.log(2);
} else {
  console.log(3)
}
// 转换为
if (1) {
  console.log(1);
} else {
  if (2) {
    console.log(2)
  } else {
    console.log(3);
  }
}

这一步是为了方便后续的遍历操作，对于一个IfStatement的语句

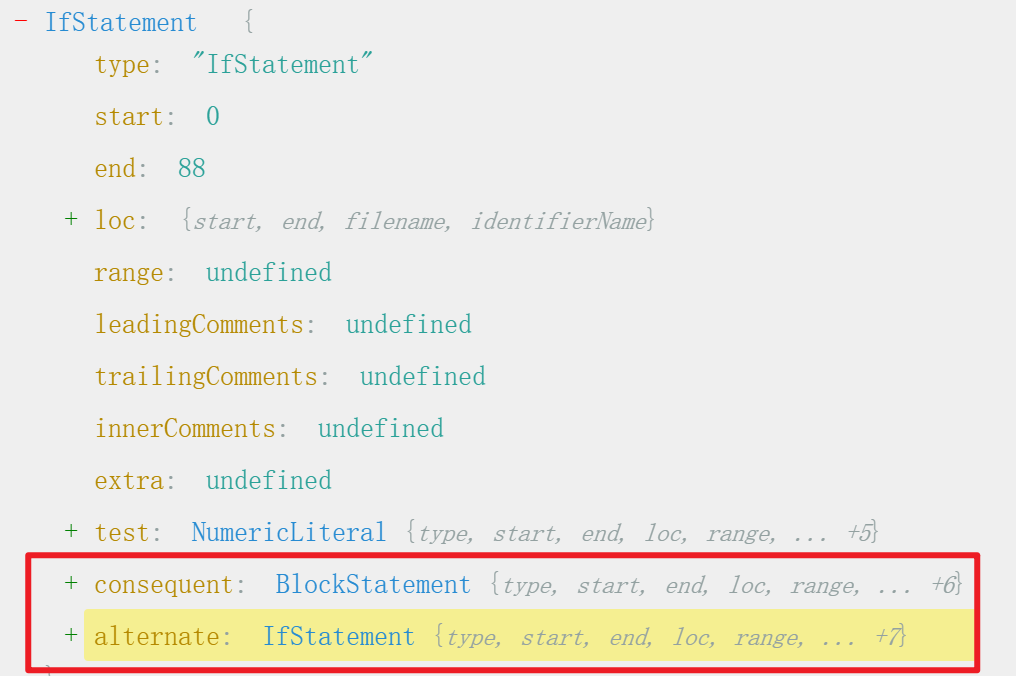
Step2-补全if...else...

为了确保IfStatement的后续节点都是BlockStatement所以就需要解决下方这样的情况：

if (!_$tg) _$ZZ += 1;

解析上方代码，可以看见consequent对应的不是BlockStatement而是ExpressionStatement。

要解决这种情况也是非常的简单，我们只需要用BlockStatement将其原本的语句给“包”起来即可。

在原来的基础上加上{} 再查看抽象树。

function step2(ast) {
  traverse(ast, {
    ExpressionStatement: funcToStr
  })

  function funcToStr(path) {
    let node = path.node;
    let parentNode = path.parent;
    // 当前节点的父节点也是IfStatement的情况
    if (isIfStatement(parentNode)) {
      path.replaceWith(blockStatement([node]));
    }
  }
}

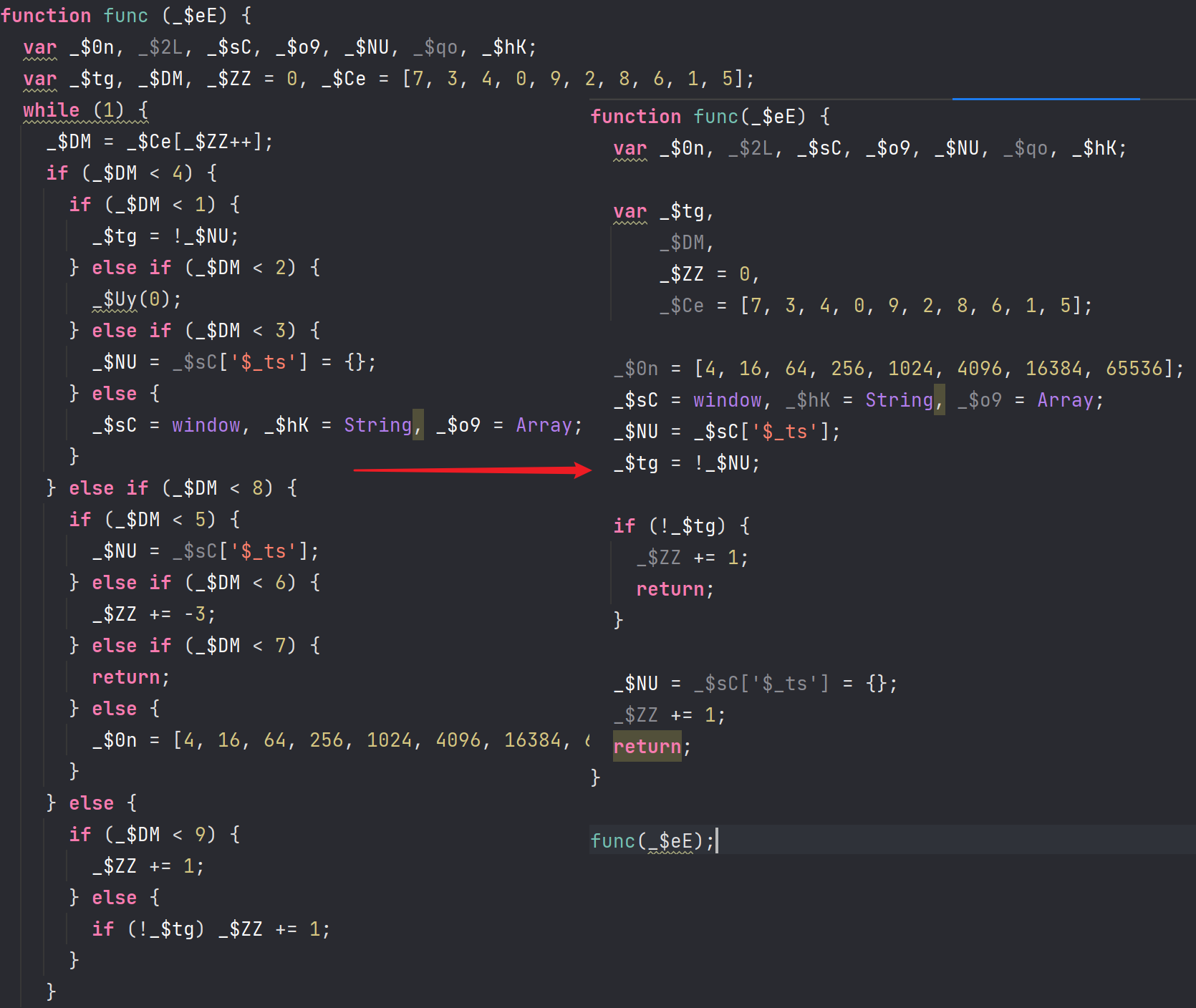
这一步处理完之后的效果如下。

function func(_$eE) {
  var _$0n, _$2L, _$sC, _$o9, _$NU, _$qo, _$hK;

  var _$tg,
      _$DM,
      _$ZZ = 0,
      _$Ce = [7, 3, 4, 0, 9, 2, 8, 6, 1, 5];

  while (1) {
    _$DM = _$Ce[_$ZZ++];

    if (_$DM < 4) {
      if (_$DM < 1) {
        _$tg = !_$NU;
      } else {
        if (_$DM < 2) {
          _$Uy(0);
        } else {
          if (_$DM < 3) {
            _$NU = _$sC['$_ts'] = {};
          } else {
            _$sC = window, _$hK = String, _$o9 = Array;
          }
        }
      }
    } else {
      if (_$DM < 8) {
        if (_$DM < 5) {
          _$NU = _$sC['$_ts'];
        } else {
          if (_$DM < 6) {
            _$ZZ += -3;
          } else {
            if (_$DM < 7) {
              return;
            } else {
              _$0n = [4, 16, 64, 256, 1024, 4096, 16384, 65536];
            }
          }
        }
      } else {
        if (_$DM < 9) {
          _$ZZ += 1;
        } else {
          if (!_$tg) {
            _$ZZ += 1;
          }
        }
      }
    }
  }
}

Step3-平坦化

执行流程既然是依靠整数数组 和下标值 ，那么我们就来先来把这两个部分提出来。

在本例中，整数数组与下标变量的赋值均是在while循环上方完成，然后我们又是需要平坦化并替换掉while节点，所以我们递归的目标就是WhileStatemtent

function step2(ast) {
  traverse(ast, {
    WhileStatement: funcToStr
  })
}

查看抽象树，可知while循环上方的赋值语句属于它的兄弟节点，如下图所示。

获取上一个兄弟节点路径和兄弟节点

var prevSiblingNodePath = path.getPrevSibling();
var prevSiblingNode = prevSiblingNodePath.node;

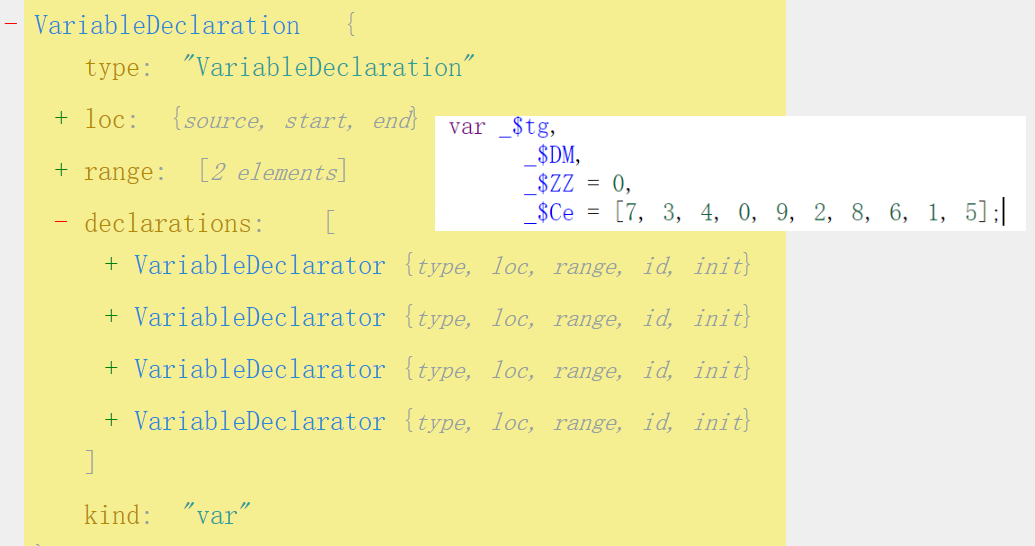
找到后节点后，获取数组和下标变量名。兄弟节点的类型是VariableDeclaration，当对一个节点的结构不熟悉时，就去可视化抽象树上看看。

可以看到declaraions中有四个变量声明符，与代码一一对应，我们所需要的就是第三个和第四个。

var node = path.node;
var prevSiblingNodePath = path.getPrevSibling();
var prevSiblingNode = prevSiblingNodePath.node;
var subscriptNameNode = prevSiblingNode.declarations[2];
var subscriptName = subscriptNameNode.id.name;
var arrNode = prevSiblingNode.declarations[3];
var arr = arrNode.init.elements;

接下来就是“模拟”while循环，平坦化执行流。

之前处理成了层层嵌套的if...else...语句，就是为了方便此时的遍历。

此时的遍历，可以看成是在遍历一颗二叉树 ，然后先写出一个大致的框架

function test(node, inx) {
  if (arr[inx] < curNode.test.right.value) {
    // 满足
  } else {
    // 不满足
  }
}

node是BlockStatement 节点，inx是数组的下标值，curNode.test.right.value就是if 表达式右边的值。

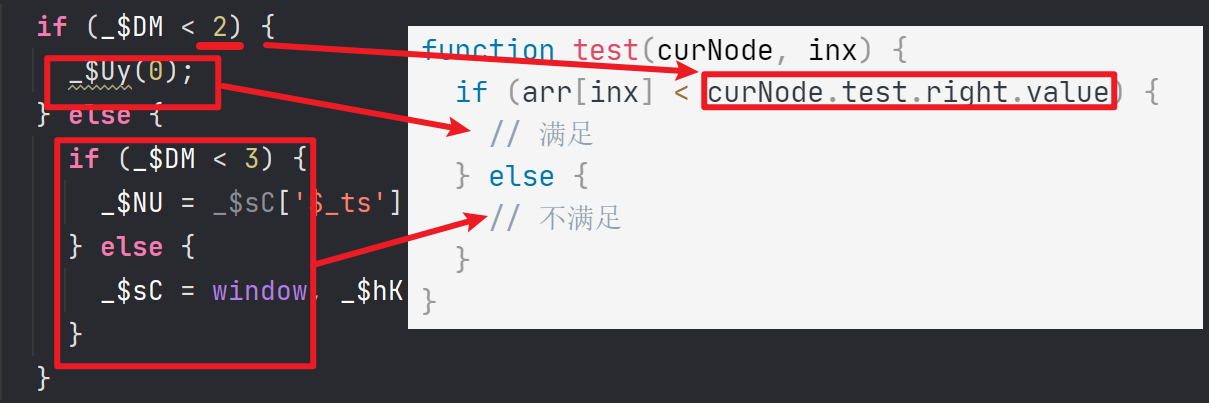
通过在第一步的操作，if后的子节点也都是BlockStatement

function test(node, inx) {
  if (t.isExpressionStatement(curNode[0])) {
    // 如果是表达式，表示已经走到底了，将表达式作为结果返回
    return node.body;
  }
  if (arr[inx].value < curNode.test.right.value) {
    // 满足
    return test(node.consequent, inx)
  } else {
    // 不满足
    return test(node.alternate, inx)
  }
}

经过上方代码，已经可以拿到第一个执行语句了，为了拿到所有的执行语句，则需要在每拿到一个语句后就对下标值+1， 然后再进行下一次遍历，直到遇到ReturnStatement。

Tips：下标值+1是每次循环的默认操作

function test(node, inx) {
  var resultBody = [];
  while (1) {
    if (t.isExpressionStatement(node[0])) {
      // 如果是表达式，表示已经走到底了，将表达式作为结果返回
      return node.body;
    }

    if (t.isReturnStatement(resultBody[resultBody.length-1])) {
      break;
    }
    
    // curNode 为IfStatement
    var curNode = node.body[1] || node.body[0];

    if (arr[inx] < curNode.test.right.value) {
      // 满足
      resultBody = resultBody.concat(test(curNode.consequent, inx));
    } else {
      // 不满足
      resultBody = resultBody.concat(test(curNode.alternate, inx));
    }
    inx += 1;
  }
  return resultBody;
}

上方代码仍有缺陷，因为while循环是写在test里面的，所以每次递归进入函数都需要进入一次while循环，但是并不是每条语句后面都有return，这就会导致死循环。

while循环的本来意义是针对最顶层的遍历，所以可以再传入递归深度，如果递归深度超过1则直接跳出while循环。

function test(node, inx, depth) {
  depth += 1;
  var resultBody = [];
  while (1) {
    if (t.isExpressionStatement(node[0])) {
      // 如果是表达式，表示已经走到底了，将表达式作为结果返回
      return node.body;
    }

    // curNode 为IfStatement
    var curNode = node.body[1] || node.body[0];

    if (arr[inx] < curNode.test.right.value) {
      // 满足
      resultBody = resultBody.concat(test(curNode.consequent, inx, depth));
    } else {
      // 不满足
      resultBody = resultBody.concat(test(curNode.alternate, inx, depth));
    }

    if (t.isReturnStatement(resultBody[resultBody.length-1]) || depth > 1) {
      // 如果深度超过1，则跳出while循环
      break
    }
    inx += 1;
  }
  return resultBody;
}

在源代码的while循环中，可能因为判断结果而影响下标值 ，例如：

  if (_$DM < 9) {
    _$ZZ += 1;
  } else {
    if (!_$tg) _$ZZ += 1;
  }

下标变量_$ZZ是否+1 取决于_$tg的值，而对于我们在外面的程序因为没有真正执行js代码所以完全不知道_$tg的值，也就无法得知这里具体是“走左还是走右”。

所以，最稳妥的方法就是考虑两种情况，分别遍历满足与不满足的两种情况，最终汇总为一个IfStatement。

1、 找到if(!_$tg)

首先它是一个IfStatement并且test为UnaryExpression

2、 计算下标值

if (t.isUnaryExpression(curNode.test)) {
  var real_val;
  if (t.isUnaryExpression(curNode.right)) {
    // 注意： 右边的值可能是负数， 例如 a += -1
    var val = curNode.consequent.body[0].expression.right.argument.value;
    var op = curNode.consequent.body[0].expression.right.operator;
    real_val = eval(`${op}${val}`);
  } else {
    real_val = curNode.consequent.body[0].expression.right.value;
  }
  // 获取操作符, += , -=
  var operator = curNode.consequent.body["0"].expression.operator;
  inx = eval(`${inx}${operator.replace('=', '')}${real_val}`);
}

3、 分别遍历两种情况

对于是否满足情况，都是继续调用递归函数，只是传入的实参不同罢了。

例如，条件为真的情况，在实际循环中，下一次遍历必将返回while的开头，所以这里传入初始节点 ，下标值传入计算出来的新值，递归深度为0。

test(initNode, inx+1, 0)

这样就可以拿到满足这个条件时的后续执行流程。

对于不满足条件的情况，按正常流程执行即可。

随后调整“亿”点点代码即可完成递归函数。

function test(node, inx, depth) {
    depth += 1;
    var resultBody = [];
    while (1) {

      if (node.body.length === 1 && t.isExpressionStatement(node.body[0])) {
        return node.body
      }

      var curNode = node.body[1] || node.body[0];

      if (t.isReturnStatement(curNode)) {
        return node.body;
      }

      if (t.isIfStatement(curNode)) {
        if (t.isUnaryExpression(curNode.test)) {
          var real_val;
          if (t.isUnaryExpression(curNode.right)) {
            // 注意： 右边的值可能是负数， 例如 a += -1
            var val = curNode.consequent.body[0].expression.right.argument.value;
            var op = curNode.consequent.body[0].expression.right.operator;
            real_val = eval(`${op}${val}`);
          } else {
            real_val = curNode.consequent.body[0].expression.right.value;
          }
          // 获取操作符, += , -=
          var operator = curNode.consequent.body["0"].expression.operator;
          inx = eval(`${inx}${operator.replace('=', '')}${real_val}`);
          resultBody = resultBody.concat([t.ifStatement(curNode.test, t.blockStatement(test(initNode, inx + 1, 0)))])
        } else if (t.isBinaryExpression(curNode.test)) {
          if (arr[inx].value < curNode.test.right.value) {
            // 满足
            resultBody = resultBody.concat(test(curNode.consequent, inx, depth));
          } else {
            // 不满足
            resultBody = resultBody.concat(test(curNode.alternate, inx, depth));
          }
        }
      }

      if (t.isReturnStatement(resultBody[resultBody.length - 1])) {
        break;
      }

      if (depth > 1) {
        break;
      }
      inx += 1;
    }
    return resultBody;
    }

平坦化结果

小结

ast这玩意儿折腾了一个星期，最烦人的部分还是写递归（算法学的差痛苦了。。。），在刚开始学习ast时，无法记住每一个节点的结构，所以需要多使用可视化工具，不清晰的结果就将代码丢进去瞧瞧。

还有一点，本文的平坦化方法不是最优解，多动手，多练习才是最有效的学习方式。

共勉！peace！

参考文章

[1] Js Ast一部曲：高完整度还原某V5的加密

[2] Js Ast二部曲：某V5 “绝对不可逆加密” 一探究竟

[3] 《JavaScript AST其实很简单》

#爬虫 8 #JS逆向 5 #瑞数 3 #AST 2
一个脚本解决CSDN远程图片转存失败的问题
JavaScript AST抽象语法树常见节点及结构