描述

给你一个数组 nums ，它包含 n 个正整数。你需要计算所有非空连续子数组的和，并将它们按升序排序，得到一个新的包含 n * (n + 1) / 2 个数字的数组。

请你返回在新数组中下标为 left 到 right **（下标从 1 开始）**的所有数字和（包括左右端点）。由于答案可能很大，请你将它对 10^9 + 7 取模后返回。

示例 1：

输入：nums = [1,2,3,4], n = 4, left = 1, right = 5
输出：13 
解释：所有的子数组和为 1, 3, 6, 10, 2, 5, 9, 3, 7, 4 。将它们升序排序后，我们得到新的数组 [1, 2, 3, 3, 4, 5, 6, 7, 9, 10] 。下标从 le = 1 到 ri = 5 的和为 1 + 2 + 3 + 3 + 4 = 13 。

示例 2：

输入：nums = [1,2,3,4], n = 4, left = 3, right = 4
输出：6
解释：给定数组与示例 1 一样，所以新数组为 [1, 2, 3, 3, 4, 5, 6, 7, 9, 10] 。下标从 le = 3 到 ri = 4 的和为 3 + 3 = 6 。

示例 3：

输入：nums = [1,2,3,4], n = 4, left = 1, right = 10
输出：50

提示：

• 1 <= nums.length <= 10^3
• nums.length == n
• 1 <= nums[i] <= 100
• 1 <= left <= right <= n * (n + 1) / 2

---

标签
#前缀和 #二分查找 #数组 #排序

相似题目

---

题解

0x01 前缀和 + 暴力遍历

最简单的做法就是按题目要求模拟，长度为 n 那就模拟 n 个子数组（前缀和），然后拼接成一个新数组，将新数组按升序排序，再通过切片求和即可。

以 nums = [1, 2, 3, 4], left = 3, right = 4 为例

图示：

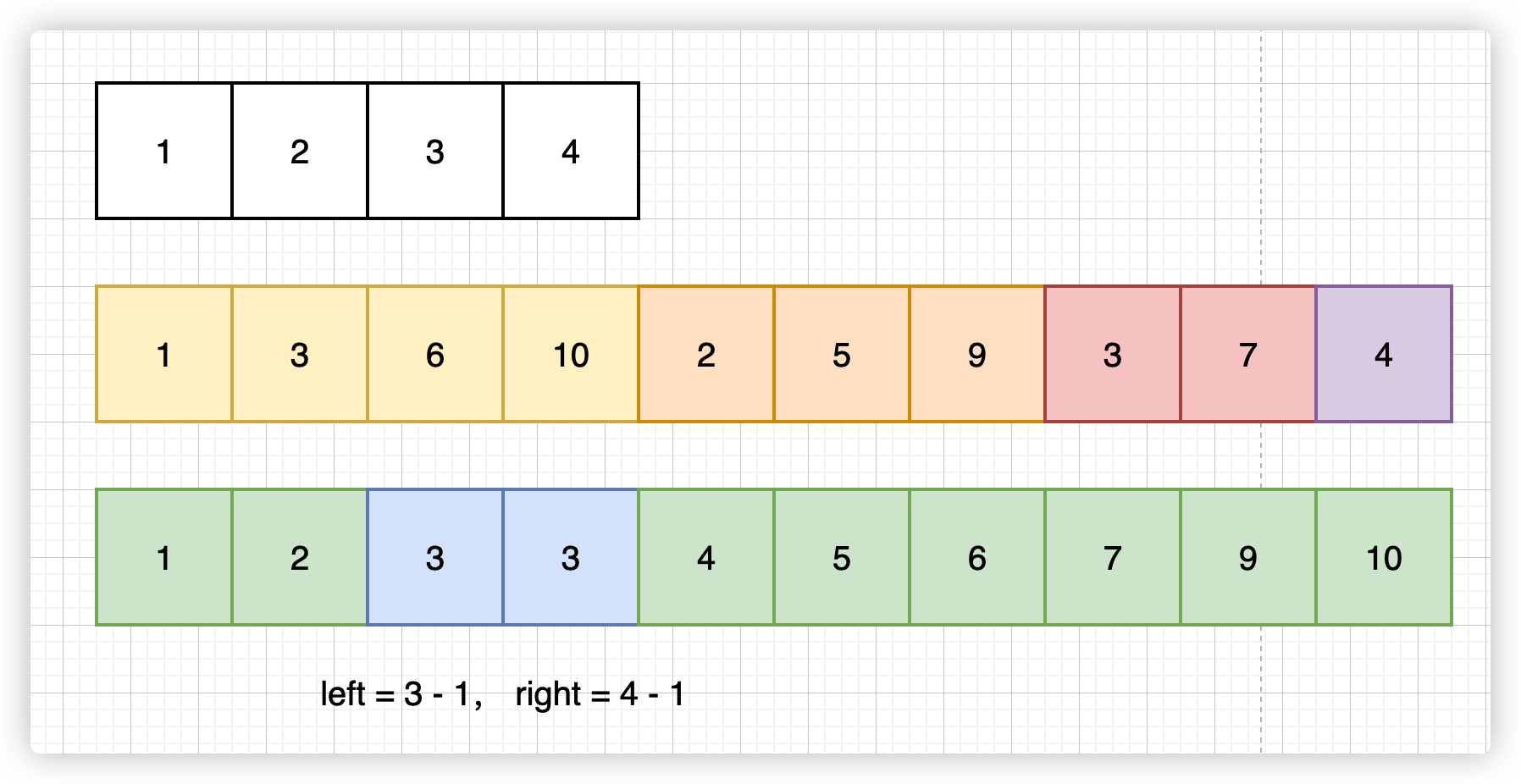
代码：

class Solution:
    def rangeSum(self, nums: List[int], n: int, left: int, right: int) -> int:
        sums = []
        for i in range(len(nums)):
            sums += list(itertools.accumulate(nums[i:]))
        sums.sort()
        return sum(sums[left-1:right]) % (10**9 + 7)

0x02 前缀和 + 二分查找

将 nums 排序，然后将其前缀和子数组排列开来，就是半个矩阵，如图所示：

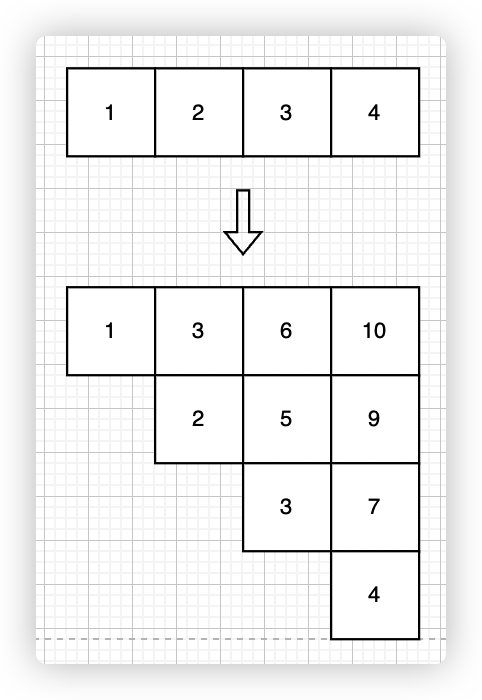
这个矩阵有如下特点：

• 从左往右单调递增
• 从上往下单调递增

题目要求算出 [left, right] 的和，问题可以转换成：

• 求 [0, left] 的和 leftSum；
• 求 [0, right] 的和 rightSum；
• rightSum - leftSum 就是答案；

来几张图一目了然：

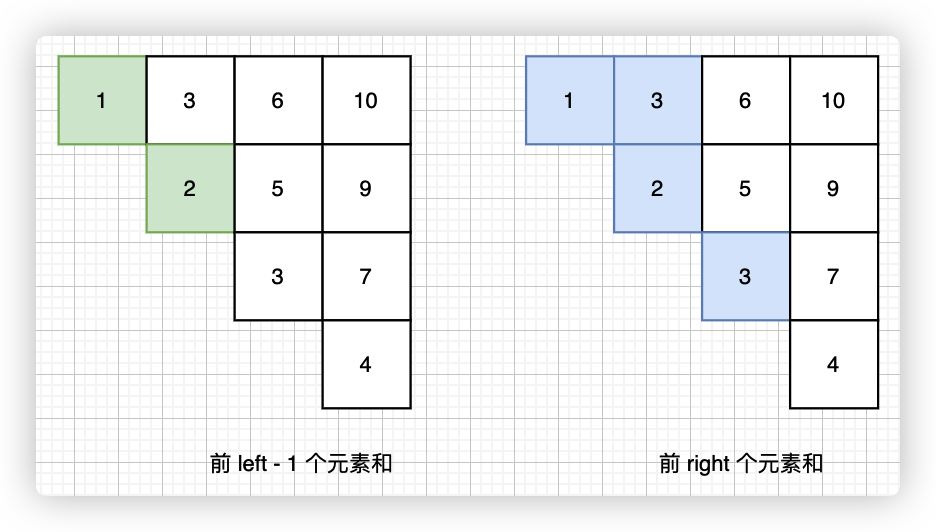
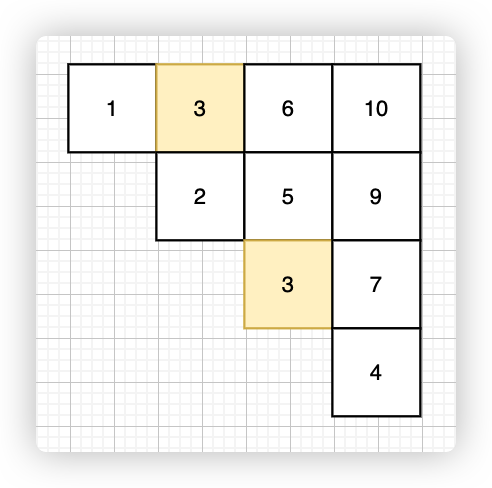
两者相减：

• left 表示求矩阵的前 left - 1 个数
• right 表示求矩阵的前 right 个数

通过上面的分析，将问题转换成了查找一个矩阵的前 K 个元素之和，但是前提条件是得把所有元素计算出来排列成一个矩阵，如果是这样，那我还不如直接暴力求解了呢。

我们求的是什么，是和，并不是某个单独的元素，即使从矩阵找到这些元素也是为了求和。

官方题解告诉我们求前缀和的前缀和，然后一系列操作，我太菜了，是直接看懵逼了。

---

先来理一理这个前缀和数组与矩阵之间藏着什么猫腻。

首先得搞明白一件事，给我们一个前缀和数组 sums = [1, 3, 6, 10]，它是数组 arr = [1, 2, 3, 4] 的前缀和，问，如何通过前缀和求出算出其他元素？

换一种描述，数组 arr 排列出来所有的前缀和为 [1, 2, 3, 3, 4, 5, 6, 7, 9, 10]，试过第一种方法对这个结果应该不会陌生吧，为了方便下文引用，就叫这个长长的数组为 long_arr

好，那现在的问题是，通过 sums = [1, 3, 6, 10] 求 long_arr 数组倒数第 2 位元素。

• sums[-1] - sums[0] = 10 - 1 = 9

可以直接通过 sums 两个和相减得出答案，再来看看求其他元素：

• 求 long_arr 倒数第 3 位： sums[-1] - sums[1] = 10 - 3 = 7
• 求 long_arr 正数第 2 位： sums[1] - sums[0] = 3 - 1 = 2

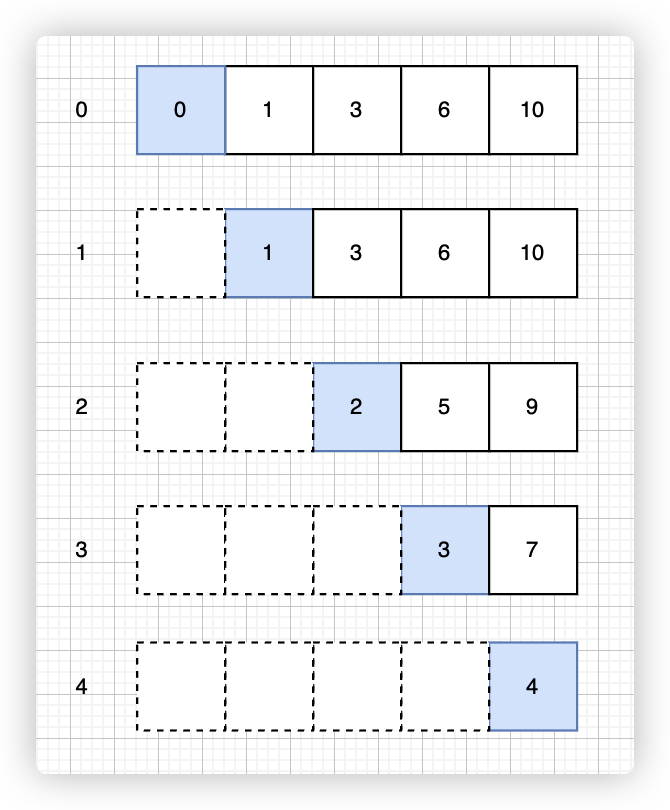
所以，有了这样一个前缀和，就相当于拥有了一个矩阵，没有理解这个相减逻辑，没关系看图就能明白了。

• 看 0 层（用 i 来表示当前层数，即 i=0），10 - 0 = 10，所以下一层（i = 1）的这个位置还是 10
• 看 1 层，10 - 1 = 9，所以下一层（i = 2）的这个位置就是 9

可以看到，每个元素和该元素所在层的第一个元素相减，就是下一层的该位置的值

每遍历一层就会少一个元素，顺着层数的增加，每一层的第一个元素都在后移。

每一层的第一个元素的位置是和层数相匹配的，看图：

• 第 0 层，第一个元素的坐标就是 (0, 0)；
• 第 1 层，第一个元素的坐标就是 (1, 0)；
• 第 2 层，第一个元素的坐标就是 (2, 0)；
• …
  

---

回到题目，还记得上面讲找一个矩阵的前 K 个元素之和吗？

这是一个矩阵，通过一个值，筛出矩阵的前 K 个数，类似于 378. 有序矩阵中第 K 小的元素 这道题。

寻找第 K 个数

通过二分查找猜出一个数，这个数就是第 K 个元素的值。

再次提醒，通过二分找到的这个元素，表示的是第 K 个元素的值。 不然写了半天，不知道为什么写二分查找，找出来是什么东西。对，说的就是我。

已知目标数 K（表示有 K 个数），猜一个数 x，找出矩阵中小于等于 x 的总数 count。

查找范围是 [0, preSums[n]]， preSums 就是原数组的前缀和，preSums[n] 就是矩阵的右上角，是该矩阵中最大的数，例如下图中的 10。

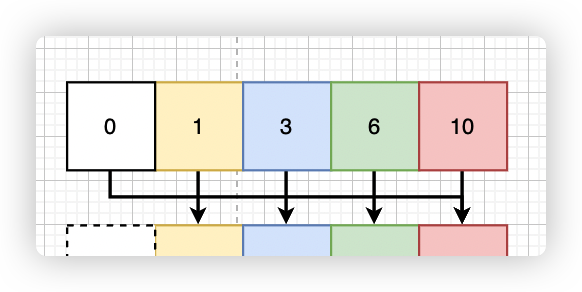
注意：前缀和下标为 0 的元素一般会用 0 占位，第 0 个元素的前缀和就是 0 ，符合直觉，方便计算。

---

那么总数怎么求？

总数就是找该矩阵中小于等于 x 的元素的总数。

对于一个真实的矩阵，相信大家应该都会，现在只是一个前缀和。上面讲了前缀和与矩阵的关系，这里就可以用上了。

在每一层遍历时，从左往右每个元素都去减第 1 个元素，差值小于等于 x 就继续右移，直至大于 x 时，表示当前层遍历结束。

我们在遍历每一层时，是通过前缀和的差值来判断是否符合小于等于 x 的，所以每一层的遍历其实是对下一层满足条件的元素个数的统计。

一层遍历结束，就可以计算下一层满足条件的元素个数为 j - i - 1， j 表示纵坐标

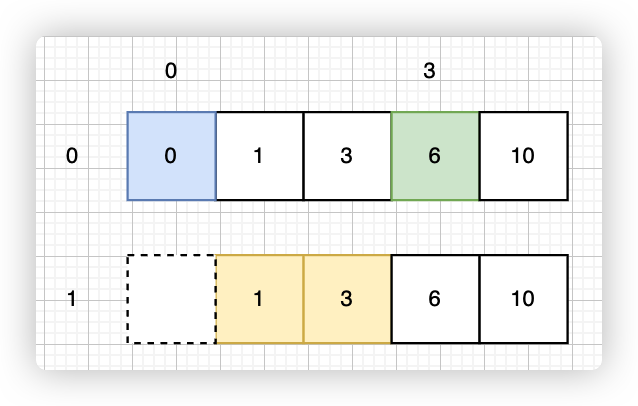
比如这里的 x 是 3， 最终不断向右移动会停在 6，6 - 0 不满足 <= 3，那么下一层满足条件的元素个数就是 3 - 0 - 1 = 2 就是两个，看图下一层（黄色块）确实就是两个数符合，也就是 i 和 j 中间的元素个数（不包含 i 和 j）

用代码实现出来就是这样：

def getCount(x: int) -> int:
	count = 0
	j = 1
	for i in range(n):
		while j <= n and prefixSums[j] - prefixSums[i] <= x:
			j += 1
		count += j - i - 1
	return count

---

现在可以根据一个值来求出矩阵中小于等于该值的元素总个数了。

二分的取值范围：[0, preSums[n]]，左闭右闭。

选择 while left <= right 作为循环条件。

接下来比较 count 与 k ：

1. 如果 count > k，说明 x 太大了，应该收缩右边界，即 right = mid - 1；
2. 如果 count < k，说明 x 太小了，应该收缩左边界，即 left = mid + 1；
3. 如果 count == k，可能刚好符合，也可能是还有更小的值，所以继续收缩右边界，即 right = mid - 1；

所以二分如下：

def getKth(k: int) -> int:
	left, right = 0, prefixSums[n]
	while left <= right:
		mid = (left + right) // 2
		count = getCount(mid)
		if count < k:
			left = mid + 1
		else:
			right = mid - 1
	return left

---

现在有了第 K 个元素的值，记为 num，接下来就是又遍历矩阵（从 0 层开始，i = 0）：

1. 每一层从左往右遍历，元素（计算方式与 getCount 中的一致）小于 num 则继续向右移动，直到不满足；
2. 一层遍历结束时，得到纵坐标 j；
3. 记录当前层符合条件的元素个数 j - i；

为什么是小于？

这个矩阵的元素是可以重复的，比如 这个数组[1, 2, 2, 3]，num = 2, k = 2，如果是小于等于就会找出三个元素 1, 2, 2，明显多出了一个 2。

那么这里判断条件是小于，先把小于 2 的元素给加上并记录其数量，最后看看等于 2 的元素还差多少个（diff = 总数量 k - 已记录数量），通过 diff * num = 1 * 2 补上即可。

所以，在每一层遍历结束时，还需记录下当前层符合条件的元素个数，也就是 j - i。

到最后所有层遍历完后，已符合条件的元素个数为 record_count，最后再加上 num * (k - record_count 即可。

---

接下来，是通过前缀和的前缀和来计算前 K 个元素的和了。

还是以 nums = [1, 2, 3, 4] 为例，它的前缀和是 preSums = [1, 3, 6, 10]，preSums 的前缀和是 prePreSums = [1, 4, 10, 20]。

我们同样把 prePreSums 展开成矩阵来看：

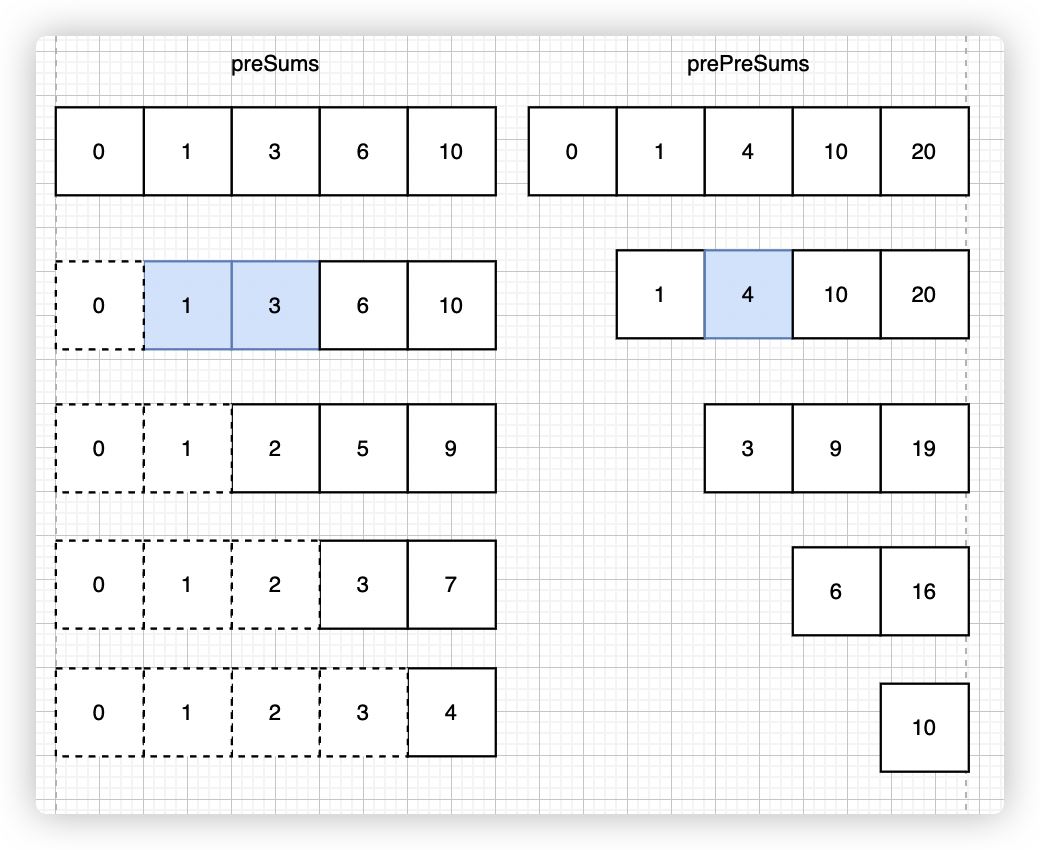
如图所示，我想求 preSums [0, 2] 的和，直接访问 prePreSums[2] 即可。

假如想求下图中绿色块的和，会发现在 prePreSums 中对应位置是 9，而不是 7。

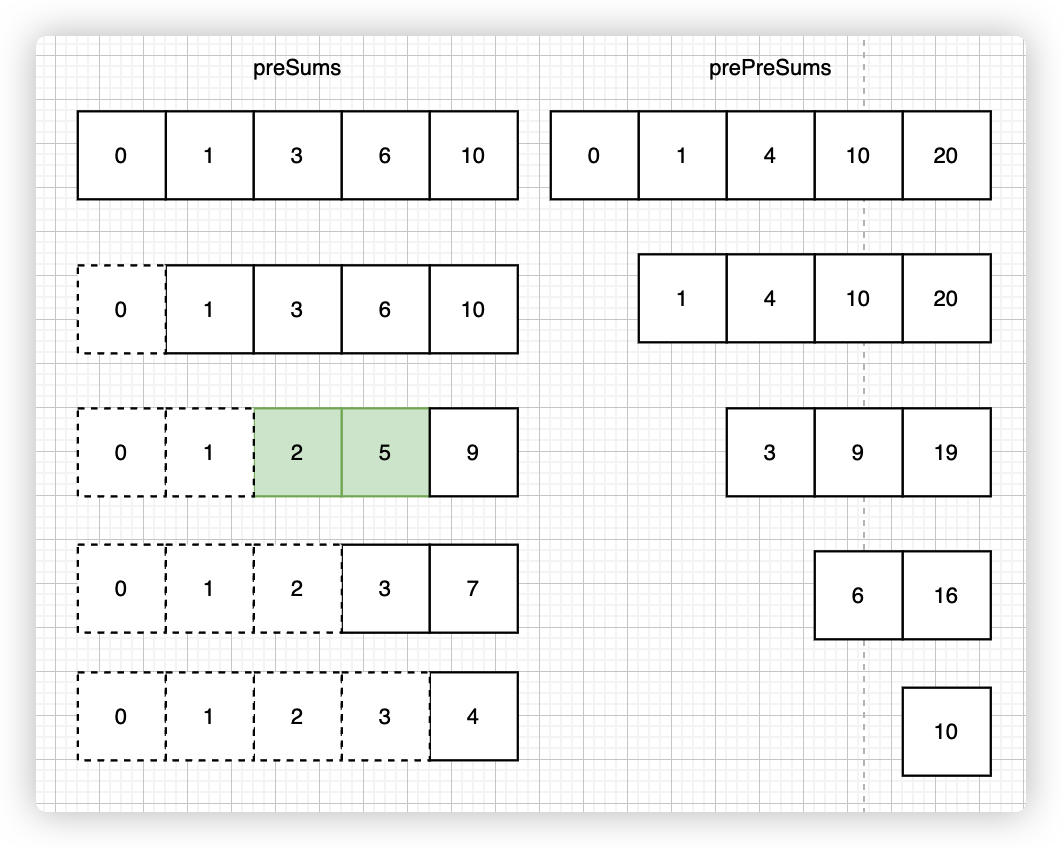
• 9 是怎么来的？ prePreSums[3] - prePreSums[1]，表示的就是 preSums[2] + preSums[3] = 3 + 6 = 9
• 2 和 5 是怎么来的？ preSums[2]- preSums[1] = 3 - 1 = 2 ，preSums[3] - preSums[1] = 6 - 1 = 5，也就是分别减去了所在层的第一个元素。

所以 7 就是通过这个公式计算而来：

prePreSums[3] - prePreSums[1] - (3 - 1) * preSums[1]

• 3 表示纵坐标，用 j 来表示
• 1 表示横坐标，用 i 来表示

换成表达式就是：

prePreSums[j] - prePreSums[i] - (j - i) * preSums[i]

至此，整个流程应该算是分析完毕了。

---

以下代码来源是官方题解，我加了部分注释。

class Solution:
    def rangeSum(self, nums: List[int], n: int, left: int, right: int) -> int:
        MODULO = 10**9 + 7
        prefixSums = [0]
        for i in range(n):
            prefixSums.append(prefixSums[-1] + nums[i])
        
        prefixPrefixSums = [0]
        for i in range(n):
            prefixPrefixSums.append(prefixPrefixSums[-1] + prefixSums[i + 1])

        def getCount(x: int) -> int:
            count = 0
            j = 1
            # 看做是遍历矩阵
            for i in range(n):
	            # i 在不断增长，所以 prefixSums[i] 一直表示都是当前层的第一个元素
                while j <= n and prefixSums[j] - prefixSums[i] <= x:
	                # 符合条件就右移
                    j += 1
                j -= 1
                count += j - i
            return count

        def getKth(k: int) -> int:
	        # 这里整个二分查找就是求左边界
			# 即找到第一个满足 count == k 的值（使count == k的最小值）
            left, right = 0, prefixSums[n]
            while left <= right:
                mid = (left + right) // 2
                count = getCount(mid)
                if count < k:
                    left = mid + 1
                else:
                    right = mid - 1
            return left

        def getSum(k: int) -> int:
            num = getKth(k)
            total, count = 0, 0
            j = 1
            for i in range(n):
                while j <= n and prefixSums[j] - prefixSums[i] < num:
                    j += 1
                # 当前 j 位置的元素是 i 行 第 1 个大于等于 num 的值
                # 我们要找的是最后一个小于 num 的元素，所以 -1
                j -= 1
	            
                total += prefixPrefixSums[j] - prefixPrefixSums[i] - prefixSums[i] * (j - i)
                # 记录当前行符合条件的个数
                count += j - i
	        # 最后补上等于 num 的部分
            total += num * (k - count)
            return total

        return (getSum(right) - getSum(left - 1)) % MODULO

小结

最近在刷二分查找的题，这道题的二分查找对我来说，真的是绕了。

刚开始看题解的时候，真的是看不进去，所以画一画图方便理解。

希望这篇题解能够帮助到你，如有纰漏欢迎指正。