描述

给你两个正整数数组 nums1 和 nums2 ，数组的长度都是 n 。

数组 nums1 和 nums2 的 绝对差值和 定义为所有 |nums1[i] - nums2[i]|（0 <= i < n）的 总和（下标从 0 开始）。

你可以选用 nums1 中的 任意一个 元素来替换 nums1 中的 至多 一个元素，以 最小化 绝对差值和。

在替换数组 nums1 中最多一个元素 之后 ，返回最小绝对差值和。因为答案可能很大，所以需要对 109 + 7 取余 后返回。

|x| 定义为：

• 如果 x >= 0 ，值为 x ，或者
• 如果 x <= 0 ，值为 -x

示例 1：

输入：nums1 = [1,7,5], nums2 = [2,3,5]
输出：3
解释：有两种可能的最优方案：
- 将第二个元素替换为第一个元素：[1,7,5] => [1,1,5] ，或者
- 将第二个元素替换为第三个元素：[1,7,5] => [1,5,5]
两种方案的绝对差值和都是 |1-2| + (|1-3| 或者 |5-3|) + |5-5| = 3

示例 2：

输入：nums1 = [2,4,6,8,10], nums2 = [2,4,6,8,10]
输出：0
解释：nums1 和 nums2 相等，所以不用替换元素。绝对差值和为 0

示例 3**：**

输入：nums1 = [1,10,4,4,2,7], nums2 = [9,3,5,1,7,4]
输出：20
解释：将第一个元素替换为第二个元素：[1,10,4,4,2,7] => [10,10,4,4,2,7]
绝对差值和为 |10-9| + |10-3| + |4-5| + |4-1| + |2-7| + |7-4| = 20

提示：

• n == nums1.length
• n == nums2.length
• 1 <= n <= 105
• 1 <= nums1[i], nums2[i] <= 105

标签
#二分查找

题解

思路来自：https://leetcode.cn/problems/minimum-absolute-sum-difference/solution/gong-shui-san-xie-tong-guo-er-fen-zhao-z-vrmq/

讲明白了才是真明白了，共同进步，如有纰漏欢迎指正。

题目读下来有两个疑问：

1. 选择哪个元素被替换？
2. 选择哪个元素用于替换？

我先给出我之前错误的解决方案：

1. 先找到 nums1 与 nums2 中绝对值差最大的那一对，即找到被替换元素的位置；
2. 找到 nums1 中最小的元素，用于替换掉上一步找到的元素。

看上去颇有道理，现实给了我一记重拳。

看看这个用例：[1,28,21] [9,21,20]

按上面的逻辑走一遍：

1. 先找绝对值差最大的一对，就是 (1, 9)，被替换的就是下标为 0 的这个位置；
2. 找到 nums1 中最小值 1，替换后还是 [1, 28, 21]；
3. 计算 绝对值差和 ，|1-9| + |28-21| + |21-20| = 16，而实际正确结果应该是 9。

正确的解法是将 28 替换为 21，最终结果就是 9。

1. 选择哪个元素被替换？
2. 选择哪个元素用于替换？

那这两个问题怎么解决呢？

那就把 nums1 中的所有元素都替换一遍，找出最合适的

这个 最合适的 怎么理解，例如 nums1 一共 3 个元素，一共替换 3 次，选中这 3 次中绝对值差和最小的那次就是正确的替换。

这又要说说第二个问题了，每次替换的时候，我怎么知道用哪个元素来替换呢？

用于替换的元素来自于 nums1 自身，选择元素也不是乱选的，需要从 nums1 中选择一个元素使得该元素与 nums2 同位置元素的绝对值差最小。

可能有点绕，来个图示：

比如这个例子，nums1 = [1,7,5] nums2 = [2,3,5]

假如现在，准备替换 7，也就是下标为 1 位置的元素，先来看一下替换前的两数绝对差值：|nums2[1] - nums1[1]| = 4，记为diff = 4。

从 [1,7,5] 中选择元素进行替换，为了使整体绝对值差和小，所以我们应该尽量选择使当前差值最小的元素。

• 选择 1，新差值 new_diff = 2；
• 选择 7，新差值 new_diff = 4；
• 选择 5，新差值 new_diff = 2；

所以，选择 1 或者 5 是更加明智的。

从一个集合中选值，猜值，还得是二分查找。

对 nums1 进行排序，每次从排序后的数组中选择一个数，使其满足与 nums2[i] 差值最小的条件。

小结一下二分逻辑：

• 搜索区间: [min(nums1), max(nums2)]
• 搜索结果: 元素大小尽量靠近 nums2[i]，把 nums2[i] 看做搜索的最大值，就是找搜索区间的最右边界

再回顾一下，上方流程：

1. 遍历 nums1 所有元素求绝对值差和；
2. 每遍历一个元素，就通过二分找出最适合用于替换当前元素的元素（与 nums2[i] 差值最小的元素）

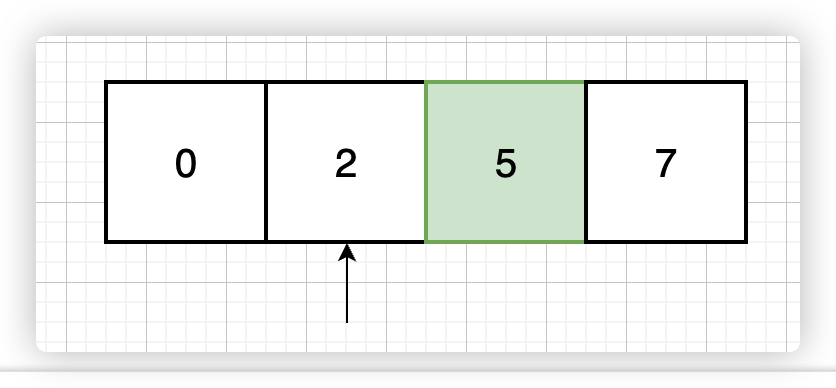
这里有个细节点，我们搜索的元素是满足 <=nums2[i] 的最大值，而差值需要再进一步的判断，比如这种情况：

通过二分找到 <=5 的最大值是 2，两者差值是 |2-5| = 3，但此时就能保证是最小差值吗？肯定不能，因为 5 后面还有一个值，得与 7 相减看看谁的差值最小嘛。

当前如果我们找到的元素就是最后一位，那自然就不用再额外比较了。

每一次遍历都会产生新的绝对值差值（new_diff），有的会比之前的绝对值差（diff）大，或小，或等于。

例如：

1. diff = 1, new_diff = 2
2. diff = 3, new_diff = 1

我们当然是选择 new_diff < diff 的情况，最终绝对值差和能减少多少就是遍历过程中 diff - new_diff 的最大值。

满足 new_diff < diff 的条件且新老差值越大，则绝对值差和越小。

0x01 二分查找

class Solution:
    def minAbsoluteSumDiff(self, nums1: List[int], nums2: List[int]) -> int:
        n = len(nums1)
        nums = copy.copy(nums1)
        nums.sort()
        # max_diff 用于保存最大(diff-new_diff)
        # sum_diff 原绝对值差值和
        max_diff = sum_diff = 0
        for i in range(n):
            a, b = nums1[i], nums2[i]
            if a == b:
                continue
            diff = abs(a - b)
            sum_diff += diff
            # 以上是正常的求和操作

            # 通过二分查找，找出一个较nums2[i]差值最小的元素
            # 即，在 nums 升序数组中，找最右边界，相减使得差值最小
            left, right = 0, n - 1
            while left <= right:
                mid = (left + right) >> 1
                if nums[mid] <= b:
                    left = mid + 1
                else:
                    right = mid - 1

            # 计算新差值
            new_diff = abs(nums[right] - b)
            # 如果不是最后一位，则需要比较比较，看看谁的值更接近nums2[i]
            if right < n - 1:
                new_diff = min(new_diff, abs(nums[right+1] - b))
            # 如果新的差值比之前的差值小，则暂存这个值
            if new_diff < diff:
                max_diff = max(max_diff, diff - new_diff)
        return (sum_diff - max_diff) % (10 ** 9 + 7)