描述

给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

示例 1:

输入: nums = [2,2,3,4]
输出: 3
**解释:**有效的组合是:
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3

示例 2:

输入: nums = [4,2,3,4]
输出: 4

提示:

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000

标签
#数组 #双指针 #排序 #二分查找 #贪心

题解

0x01 排序 + 双指针

1. 先将数组升序排序；
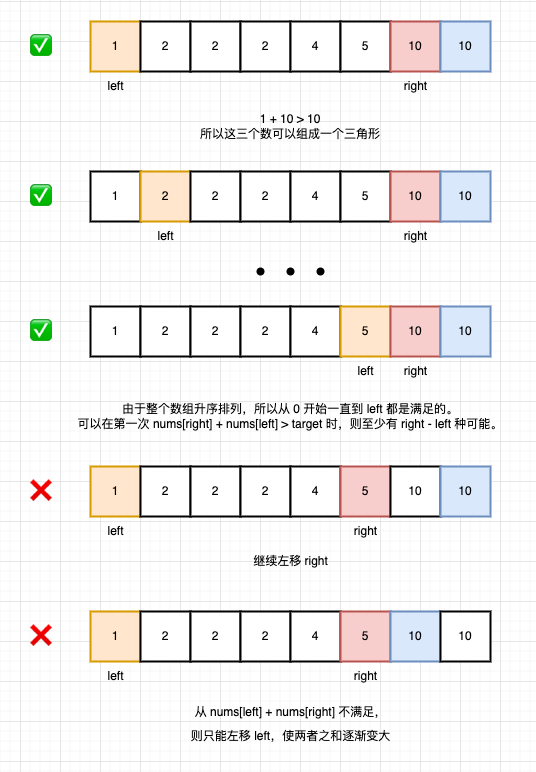
2. 逆序遍历，遍历到的每一位，用其前一位的值（红色块，left 所在位置）与最左位置的值（默认为0 号位，橙色块，right 所在位置）相加之和与当前遍历到的值做比较（蓝色块）
   1. 如果两者之和大于当前值，则可以构成三角形，那么 right - left 的值，就是这个区间内的所有可能性，这个不难理解，因为这个数组是升序的嘛。一个最小值+一个最大值都已经满足了条件，那么最小值后面直到最大值之前的值肯定也满足条件。
      1. 上一步尝试的是 最小值+最大值，所以可以左移 right 以减小两者之和，直到两者之和不满足条件
   2. 如果两者之后小于或等于当前值，则不能构成三角形，不能构成的原因就是两者之和太小了，right 所在位置已经是最大值了，所以只能让 left 所在位置的值变大，那么整体的和才会变大，也就是让 left 向右移动。

class Solution:
    def triangleNumber(self, nums: List[int]) -> int:
        nums.sort()
        res = 0
        for cur in range(len(nums)-1, 0, -1):
            left, right = 0, cur - 1
            while left < right:
                if nums[left] + nums[right] > nums[cur]:
                    res += right - left
                    right -= 1
                else:
                    left += 1
        return res

0x02 排序 + 二分查找

在上一个方法中，我们是固定一个数，然后确定另外两个数的区间。
这个方法则是，先固定两个数，再通过二分查找另一个数的最大值。

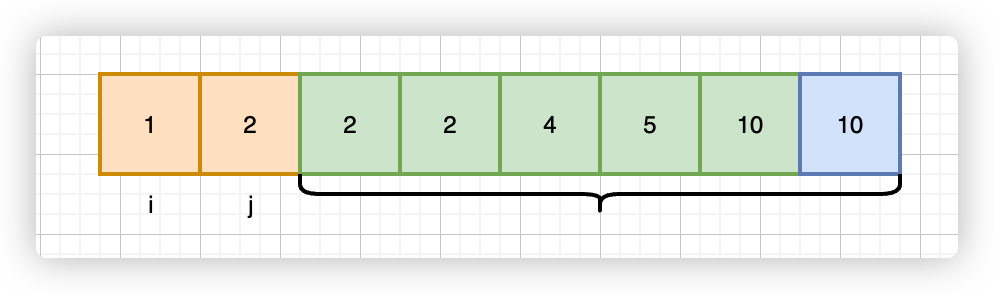
我们有一个用于比较的值，就是 nums[i] + nums[j]，必须要一个数大于这两者之和，才可以组成三角形。

接下来就使用二分查找从后面这个区间内，找出一个满足大于两者之和这个条件的最大值。 这个最大值默认就是 nums[len(nums) - 1]，即这个数组的最后一位。

这个区间是 [j+1, len(nums)-1]，这个还是蛮清楚的吧，

二分查找内的条件判断如下：

1. 如果中间值(nums[mid])小于两者之和(nums[i] + nums[j])，则说明满足三角形的构造条件，暂存下 mid 的值，为了确保 mid 之后仍有符合条件的值，左边界右移(mid + 1)
2. 否者中间值大于或等于两者之和，不满足条件，右边界左移(mid-1)。
3. 本次循环的结果就是，最大值位置 - 第二值的位置，这就是本次遍历的满足三角形的构造的数量，如图，找到的最大值是 10，从第二个值（2）的位置到最大值的位置，就是本次遍历的符合条件的个数。
   

class Solution:
    def triangleNumber(self, nums: List[int]) -> int:
        nums.sort()
        nl = len(nums)
        ans = 0
        for i in range(nl):
            for j in range(i + 1, nl):
                left, right, k = j + 1, nl - 1, j
                while left <= right:
                    # nums[i] + nums[j]
                    # 匹配到的值必须大于这个和，才能构成三角形
                    mid = (left + right) // 2
                    if nums[i] + nums[j] > nums[mid]:
                        k = mid
                        left = mid + 1
                    else:
                        right = mid - 1
                ans += k - j
        return ans